(21)いまさら聞けない「分離度を改善させる有効な方法」

ここでは、分離度を効率よく改善する方法について、理論段数、保持係数、分離係数のパラメータに着目して解説していきたいと思います。 

分離度（R）と理論段数（N）、保持係数（ｋ）及び分離係数（α）との間には、式1の関係があります。 

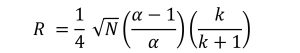
分離度(R)　式1

 いきなり数式を出してすみません。しかし、それほど難しくはありません。 

分離度は、理論段数Nの平方根に比例しています。 

例えば、理論段数10,000 段のカラムを使って分離度が1.0であったとします。分離度を1.5（完全分離）にしようとすると、理論段数は2.25倍（22,500 段のカラム）にしなければなりません。カラムの長さを２倍にしても達成出来ないので、この場合は、別のカラムを選択したほうがよさそうです。 

保持係数kは、空間補正保持時間とホールドアップタイムの比と定義されますが、ざっくり「保持時間」と考えてください。 kとk／(1+k)の関係を図１に示しました。保持時間を長くすることは分離度を改善するに有効そうです。 

保持係数を大きくするには、溶出力の小さい移動相に変更すること、逆相HPLCでは有機溶媒比率を下げればよいことになります。 

しかし、図１が示す通り、保持係数が分離度向上に大きく寄与するのは溶出の早いピークであり、保持係数が3のピークを9にしても分離度は1.2 倍にしかなりません。 

（k =3の時k／(1 + k) = 0.75、k = 9の時k／(1 + k)=0.9であり、分離度は1.2倍。） 

保持が十分なピークでは、保持係数を大きくしても、分離度はそれほど改善されず、分析時間が長くなってしまうだけになります。 

分離係数αは、2つのピークの保持係数の比のことです。
αと(α — 1)/αとの関係は図２のようになり、分離係数は1から1.2程度までほとんど直線的に分離度向上に寄与することがわかります。 

例えば、分離度1.0での分離係数が1.1の場合、分離係数が1.2になれば分離度1.5以上になります。
（α=1.1の時(α — 1)／α = 1／11、α=1.2の時(α — 1)／α = 1／6であり、分離度は1.8倍改善されます。） 

このことから分離係数は、分離度向上には効率的なパラメータであることが分かります。 固定相、移動相のpHや有機溶媒の種類、カラム温度等の様々な条件で変化させることが出来ます. 

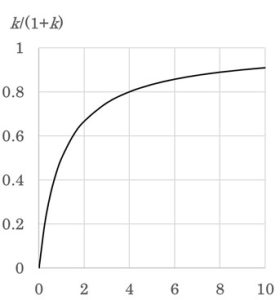
図１　保持係数kとk/(1+k)の関係

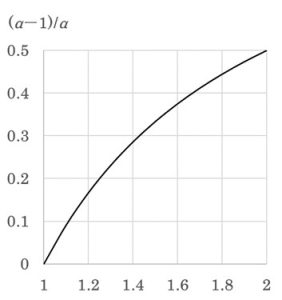
図２　分離係数αと(α－1)/αの関係

Follow me!