(27)検量線の重み付け

今回は、検量線の重み付けについて解説します。 

 　LC/MS/MSのデータ処理で、「検量線の重み付けとして1/x2や1/xを使用」することがあります。これはどういうことなのでしょうか。 

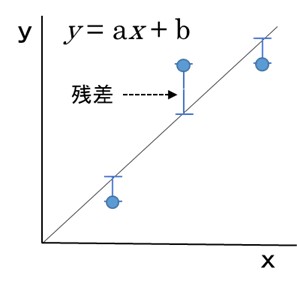
図1　測定値と回帰直線の関係

　図１のように横軸（ｘ）には、独立変数としてばらつきが無いもの（濃度）を、縦軸（ｙ）には、従属変数としてばらつきのあるもの（測定値）をプロット（●）します。回帰式とはプロットした点と回帰直線の縦方向の差（残差）を最小にした式で、これが検量線となります。 

　図１のような直線の検量線の作成には、一般的に最小二乗法を利用しますが、これは図2Aのように全濃度で誤差が一定という前提で作成されています。さらに詳しく言えば、最小二乗法では、誤差が以下の仮定が前提となっています。 

• 等分散性：誤差の母分散は全て等しい 
• 不偏性：誤差の期待値は０である 
• 無相関性：誤差は互いに無相関である 
• 正規性：誤差は正規分布に従う 

　しかし、実際の測定では、図2Bのように、低濃度や高濃度でばらつきが大きくなっていることがあります。特にLC/MS/MSで広い濃度範囲をカバーしようとしたときに、しばしば観測される現象で、これは「等分散性が満たされない」状態といえます。 

各濃度ｘiの測定値yiの分散の逆数で補正すれば、それぞれの濃度でのばらつきの違いが検量線に与える影響を打ち消す（等分散にする）ことが出来るはずですが、現実的でありませんので、分散値の変化を推定して補正をかける処理がなされます。 これを「重み付け」といい、この検量線を「重み付け検量線」といいます。 

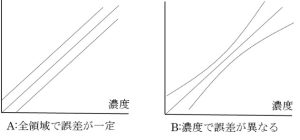
図2　検量線と誤差の関係

  重み付けには、多くの分析機器で1/xまたは1/x2が使用されています。 

 〇「濃度ｘi にｙの標準偏差σが比例する」と仮定できるとき、1/x2の重みを使用する。 

図3Aのように濃度とσが比例する場合、残差の平均が０で、分散(xiσ)2 が正規分布に従うとすると、各濃度での誤差の分布は、εi~N (0, (xiσ)2 )で表されます。分散は、(xiσ)2 = xi2σ2となるので、分散ｘi2σ2 を一定にするための重みは、wi = 1/xi2となります。 

〇「濃度ｘi にｙの分散σ2が比例する」と仮定できるとき、1/xの重みを使用する。 

図3Bのような関係の誤差がある場合で、このときの各濃度の誤差の分布は、εi~N (0, xiσ2)で表され、分散ｘiσ2 を一定にするための重みは、wi=1/xiとなります。 

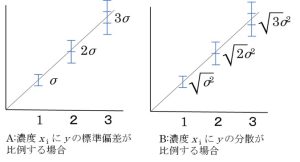
図3　2 種類の重み付けの解説

Follow me!