(39) 続・検査で用いる統計　①オッズとオッズ比

　統計で用いるオッズはギャンブル用語（？）とはずいぶん意味合いが異なります。 

オッズとは、ある事象が起きる確率pとその事象が起きない確率(1 − p)との比で、ある事象の起こりやすさを表す指標です。

〇　オッズ＝p／(1 − p)

式から分かるように、起こる確率と起こらない確率が同じ（p＝0.5）とき、オッズは１となります。１よりも大きいとその事象が起こりやすい、小さいと起こりにくいことになります。 よく示される例ですが、喫煙とがん発症の関係でオッズを説明してみましょう。 

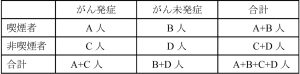
p：喫煙をしていた集団の中でガンを発症した割合　p＝A／(A＋B)
1－p：喫煙をしていた集団の中でガンを発症していない割合　1－p＝B／(A＋B) 

 同様に非喫煙者ががんを発症するオッズは、

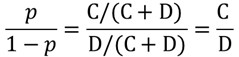となります。 

 数値といっても便宜的なものですが、実際に計算してみましょう。

この例では、喫煙者ががんを発症するオッズは0.5で非喫煙者ががんを発症するオッズは0.125となります。 

オッズ比（odds ratio, OR）とは、ある事象の起こりやすさを2つの群で比較して示す統計学的な尺度で，文字どおり、それぞれの群のオッズの比です。つまり、結果（所見の有無）に対してどれぐらい要因（検査や行動など）が寄与しているかを表します。
喫煙ががん発症にどれくらい寄与しているかをオッズ比から理解することができます。 

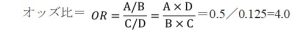
ある群における事象の起こりやすさが別の群よりも大きい場合、オッズ比は1より大きくなります。この例では（架空の数字です）喫煙者のほうが非喫煙者よりもがんになりやすいことを示しています。 

オッズ比は、疫学研究である因子（環境・食べ物・嗜好品等）がある病気の原因であるかどうかの調査でよく使用されます。オッズ比が高いほど、その因子が病気との関連性が高いことを示唆しています。 

Follow me!